Author: Lars Hellström <[email protected]>
Type: Project
State: Final
Tcl-Version: 8.5
Vote: Done
Created: 25-Jan-2004
Post-History:
Tk-Ticket: 886240
Abstract
This document proposes a new -smooth method for line and polygon canvas items that supports cubic Bezier curves and clarifies some of the existing terminology in that area.
Proposal
A new method for the -smooth canvas item option will be defined. Under this method, the points defining the item will be interpreted as a sequence knot-point control-point control-point knot-point control-point control-point ... of a curve composed of cubic Bezier segments. More precisely, if the list of coordinates is
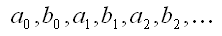
then the N_th (counting from zero) segment of the curve consists of points whose coordinates _(x,y) satisfies
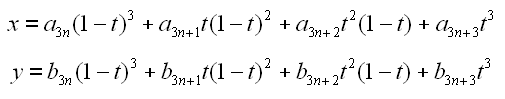
for some value of t between 0 and 1, inclusive. If there are 3N+1 points then the above defines an N segment curve. In the case that the number of points is 3N or 3N-1 then they shall still define an N segment curve, where in the first case the first knot of the first segment is reused as the last knot in the last segment, and in the second case the first knot and control point in the first segment are reused as the last control point and knot in the last segment respectively.
Straight line segments in the curve can be encoded as a segment where the control points are equal to the neighbouring knot points. While this is not the only way to encode a straight line, it is a case that is recognised and handled more efficiently by code that renders the canvas item.
The name of this new method should be "raw".
The name of the existing -smooth method (as returned by the itemcget widget command) should be changed from "bezier" to "true", and the name "bezier", while at least in Tcl 8.5 still supported, should be deprecated.
Rationale
Cubic Bezier curves, being for example the native curve format in Postscript and its descendants, is probably the most common format for smooth curves in computing today. It is even used internally in Tk; for each segment of a -smooth 1 curve, rendering starts with the calculation of a cubic Bezier representation of that curve and continues to use only this representation when approximating the smooth curve with straight line segments. Hence it might be claimed that the cubic Bezier curve is the "raw" format of a smooth curve in Tk. No new calculations need to be implemented in the core to implement this TIP, it is merely a matter of combining existing functions in a suitable way and move data around. Therefore it seems a waste to not provide cubic Bezier curves, when they are anyway already half implemented.
The reason for the interpretation of a curve with 3N points given is that this will cause the curve to be closed. Conversely, omitting the final knot point is sometimes used as a way of encoding the fact that the curve should be closed. This rule will therefore facilitate the use of data where then omitted endpoint convention has been employed. The only reason for the 3N-1 point rule is that it fits a simple scheme (when at the end of the list of coordinates, continue from the start) that supports the 3N and 3N+1 cases.
The reason for deprecating the name "bezier" for the traditional smoothing method is that it is at best confusing, and according to many authorities simply wrong. The term "Bezier curve" is very often used as a synonym of "cubic Bezier curve", whence the majority of programmers new to this feature of the canvas widget would probably expect "-smooth bezier" to imply the effect of the smoothing option proposed in this document rather than the smoothing via quadratic splines that it currently is. The amount of disappointment that could result from the unpleasant discovery that what one thought was the former is really the latter should not be underestimated.
The reason for changing the official name of the traditional smoothing method to "true" are (i) that it is backwards compatible in the sense that this name works for specifying that smoothing method in all Tk versions and (ii) that it is somewhat mnemonic, because it happens to coincide with the format used for curves in _True_Type fonts.
Background
The question of what may rightfully be called "bezier" is somewhat complicated and deserves expounding upon. It really begins with Bernstein; the Bernstein degree n form of a polynomial f is
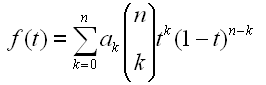
One advantage this form has over the standard form is that the coefficients a_0, ..., a_n are directly comparable to the function values f(0), f(1/n), f(2/n), ..., f(1); the two are generally not equal (with the exception for the endpoints of the [0,1] interval), but the function values approximates the sequence of coefficients in various useful ways. (Bernstein used it to give an elegant proof of the Weierstrass Approximation Theorem.)
A Bezier curve (or Bernstein-Bezier curve, as it is sometimes called) of degree n is a parametric curve P defined by a sequence of n+1 points P_0, ..., P_n (known as the control points of the curve) where each coordinate function is the Bernstein polynomial one gets by taking as a_k the corresponding coordinate of the point P_k and parametric time goes from 0 to 1; formally
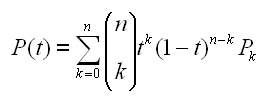
for t between 0 and 1 inclusive. Higher degree Bezier curves are not used much in computer graphics (probably because the effect on the curve of moving an single control point is often not intuitively clear) but they do exist and it is not illogical to expect that a
$canvas create line $points -smooth bezier
should be the degree-[expr {[llength $points]/2 - 1}] Bezier curve defined by the given points.
Another term which often occurs when discussing computer graphic curves is "spline". A spline is a curve that passes through a set of given points (the knots of the curve) in a given order, satisfies some smoothness condition, and in some sense is best possible under these conditions. The most common optimality condition is that the curve should be composed from segments that can be parameterized by polynomials of given degree, but there are implicit conditions (minimizing some suitable measure of curve deformation) which leads to the same family of curves.
The -smooth 1 curves of the Tk canvas are splines (of degree 2) in this sense, even though the points used for defining them are (with the exception for endpoints) not the knots of the spline. (Rather, the internal knots are the midpoints of the line segments joining two adjacent control point.) The raw curves proposed here are in general not splines (because they admit discontinuous changes in tangent direction, thus violating the smoothness condition), but they often serve as an encoding for pre-computed degree 3 splines and this use has lead to a confusion in terminology in this area. It is not uncommon that piecewise cubic Bezier curves in general are referred to as "cubic splines", even though that is a more special concept. It may also be observed that the endpoints of the Bezier segments are usually referred to as knots of the curve, whereas the term "control points" is often reserved for the non-knot control points. This rather harmless convention is for example used above. Incorrect use of the word "spline" should however be avoided.
Alternatives
It would be possible to provide the suggested functionality using a compiled extension instead, but that seems a waste since almost all of the functionality is present in the core anyway.
It would also be possible to use the semantics of the Tkspline package http://www.graphviz.org/cgi-bin/man?tkspline -smooth method providing cubic Bezier curves, but that package reverts to using the -smooth true method of smoothing if the number of points is not 3N+1, which doesn't seem useful and may cause bugs to be less visible. Using the Tkspline syntax (calling the -smooth method "spline") should probably be avoided even if the two methods were compatible, since the curves produced in general aren't splines.
Implementation
A sample implementation of this proposal (minus the part about changing the name of the existing -smooth method) exists http://sf.net/tracker/?func=detail&aid=886240&group_id=12997&atid=312997 .
Copyright
This document has been placed in the public domain.